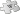Projective space

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seems to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seems to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, point and lines are primitive entities the are related by the incidence relation 'a point is on a line' or 'a line passes through a point', which is subject to at the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the following definition, which is more often encountered in modern textbooks. Using linear algebra, a projective space of dimension n is defined as the set of the vector lines (that is, vector subspaces of dimension one) in a vector space V of dimension n + 1. Equivalently, it is the quotient set of V {0} by the equivalence relation 'being on the same vector line'. As a vector line intersects the unit sphere of V in two antipodal points, projective spaces can be equivalently defined as spheres in which antipodal points are identified. A projective space of dimension 1 is a projective line, and a projective space of dimension 2 is a projective plane. Projective spaces are widely used in geometry, as allowing simpler statements and simpler proofs. For example, in affine geometry, two distinct lines in a plane intersect in at most one point, while, in projective geometry, they intersect in exactly one point. Also, there is only one class of conic sections, which can be distinguished only by their intersections with the line at infinity: two intersection points for hyperbolas; one for the parabola, which is tangent to the line at infinity; and no real intersection point of ellipses. In topology, and more specifically in manifold theory, projective spaces play a fundamental role, being typical examples of non-orientable manifolds. As outlined above, projective spaces were introduced for formalizing statements like 'two coplanar lines intersect in exactly one point, and this point is at infinity if the lines are parallel.' Such statements are suggested by the study of perspective, which may be considered as a central projection of the three dimensional space onto a plane (see Pinhole camera model). More precisely, the entrance pupil of a camera or of the eye of an observer is the center of projection, and the image is formed on the projection plane. Mathematically, the center of projection is a point O of the space (the intersection of the axes in the figure); the projection plane (P2, in blue on the figure) is a plane not passing through O, which is often chosen to be the plane of equation z = 1, when Cartesian coordinates are considered. Then, the central projection maps a point P to the intersection of the line OP with the projection plane. Such an intersection exists if and only if the point P does not belong to the plane (P1, in green on the figure) that passes through O and is parallel to P2. It follows that the lines passing through O split in two disjoint subsets: the lines that are not contained in P1, which are in one to one correspondence with the points of P2, and those contained in P1, which are in one to one correspondence with the directions of parallel lines in P2. This suggests to define the points (called here projective points for clarity) of the projective plane as the lines passing through O. A projective line in this plane consists of all projective points (which are lines) contained in a plane passing through O. As the intersection of two planes passing through O is a line passing through O, the intersection of two distinct projective lines consists of a single projective point. The plane P1defines a projective line which is called the line at infinity of P2. By identifying each point of P2 with the corresponding projective point, one can thus say that the projective plane is the disjoint union of P2 and the (projective) line at infinity. As an affine space with a distinguished point O may be identified with its associated vector space (see Affine space § Vector spaces as affine spaces), the preceding construction is generally done by starting from a vector space and is called projectivization. Also, the construction can be done by starting with a vector space of any positive dimension.