Dijkstra's algorithm

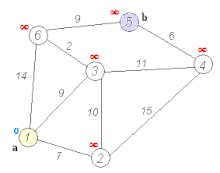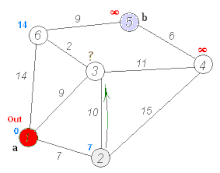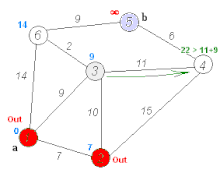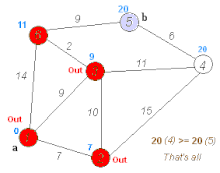
Dijkstra's algorithm (or Dijkstra's Shortest Path First algorithm, SPF algorithm) is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.What is the shortest way to travel from Rotterdam to Groningen, in general: from given city to given city. It is the algorithm for the shortest path, which I designed in about twenty minutes. One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking about whether I could do this, and I then designed the algorithm for the shortest path. As I said, it was a twenty-minute invention. In fact, it was published in ’59, three years later. The publication is still readable, it is, in fact, quite nice. One of the reasons that it is so nice was that I designed it without pencil and paper. I learned later that one of the advantages of designing without pencil and paper is that you are almost forced to avoid all avoidable complexities. Eventually that algorithm became, to my great amazement, one of the cornerstones of my fame.Problem 2. Find the path of minimum total length between two given nodes P {displaystyle P} and Q {displaystyle Q} . Dijkstra's algorithm (or Dijkstra's Shortest Path First algorithm, SPF algorithm) is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later. The algorithm exists in many variants. Dijkstra's original algorithm found the shortest path between two given nodes, but a more common variant fixes a single node as the 'source' node and finds shortest paths from the source to all other nodes in the graph, producing a shortest-path tree. For a given source node in the graph, the algorithm finds the shortest path between that node and every other.:196–206 It can also be used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined. For example, if the nodes of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road (for simplicity, ignore red lights, stop signs, toll roads and other obstructions), Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. A widely used application of shortest path algorithm is network routing protocols, most notably IS-IS (Intermediate System to Intermediate System) and Open Shortest Path First (OSPF). It is also employed as a subroutine in other algorithms such as Johnson's. The Dijkstra algorithm uses labels that are positive integers or real numbers, which are totally ordered. It can be generalized to use any labels that are partially ordered, provided the subsequent labels (a subsequent label is produced when traversing an edge) are monotonically non-decreasing. This generalization is called the Generic Dijkstra shortest-path algorithm. Dijkstra's original algorithm does not use a min-priority queue and runs in time O ( | V | 2 ) {displaystyle O(|V|^{2})} (where | V | {displaystyle |V|} is the number of nodes). The idea of this algorithm is also given in Leyzorek et al. 1957. The implementation based on a min-priority queue implemented by a Fibonacci heap and running in O ( | E | + | V | log ⁡ | V | ) {displaystyle O(|E|+|V|log |V|)} (where | E | {displaystyle |E|} is the number of edges) is due to Fredman & Tarjan 1984.This is asymptotically the fastest known single-source shortest-path algorithm for arbitrary directed graphs with unbounded non-negative weights. However, specialized cases (such as bounded/integer weights, directed acyclic graphs etc.) can indeed be improved further as detailed in Specialized variants. In some fields, artificial intelligence in particular, Dijkstra's algorithm or a variant of it is known as uniform cost search and formulated as an instance of the more general idea of best-first search. Dijkstra thought about the shortest path problem when working at the Mathematical Center in Amsterdam in 1956 as a programmer to demonstrate the capabilities of a new computer called ARMAC. His objective was to choose both a problem and a solution (that would be produced by computer) that non-computing people could understand. He designed the shortest path algorithm and later implemented it for ARMAC for a slightly simplified transportation map of 64 cities in the Netherlands (64, so that 6 bits would be sufficient to encode the city number). A year later, he came across another problem from hardware engineers working on the institute's next computer: minimize the amount of wire needed to connect the pins on the back panel of the machine. As a solution, he re-discovered the algorithm known as Prim's minimal spanning tree algorithm (known earlier to Jarník, and also rediscovered by Prim). Dijkstra published the algorithm in 1959, two years after Prim and 29 years after Jarník. Let the node at which we are starting be called the initial node. Let the distance of node Y be the distance from the initial node to Y. Dijkstra's algorithm will assign some initial distance values and will try to improve them step by step.